Bölüm 2: Fraktal varoluşun dayanılmaz hafifliği.

“Kadının yaşadığı dram, ağırlığın değil hafifliğin dramıydı. Ona düşen şey yük değil, varlığın dayanılmaz hafifliğiydi.”

Milan Kundera

”Gereklilik, ağırlık ve değer birbirinden ayrılmaz biçimde örülmüş üç kavramdır; sadece gereklilik ağırdır ve sadece ağır olan şey değerlidir.” 

O kadar karmaşık bir doğada yaşıyoruz ki varoluşun basit bir prensip üzerine kurulmuş olmasına ihtimal bile vermiyoruz. Basitlik bize değersiz geliyor. Karmaşıklık seviyoruz.

Fraktal geometrinin hayatımızdaki vazgeçilmez, “hafif ama değerli”, akıllara durgunluk verici yapısı….

Aşağıdaki şekillere benzer, birbirini sonsuz tekrar eden şekillere denk gelmişsinizdir.

Yukarıdaki eşkenar üçgen gibi ama farklı, basit bir şekil seçin. Bu şekli belli bir kurala bağlı olarak sürekli olarak tekrar edin. Tekrar sayısı artıp belli sayıya ulaşınca , ortaya çıkan yeni şekil ilk başta seçilen şekile benzeyecek. Büyük şekil, küçük şekil ile aynı ve büyük şeklin detayında sadece ana şeklin kendisi olacak.

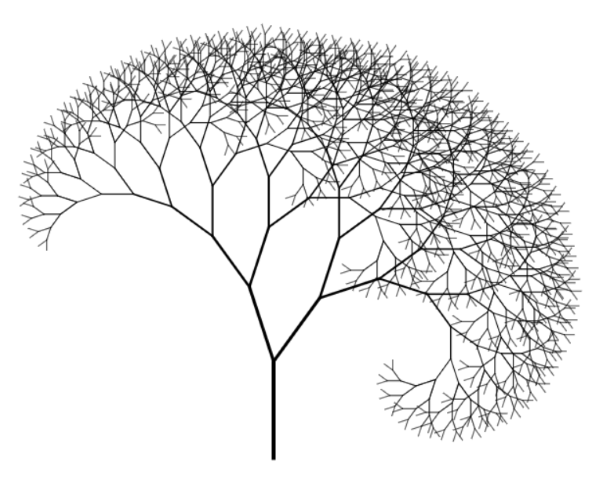
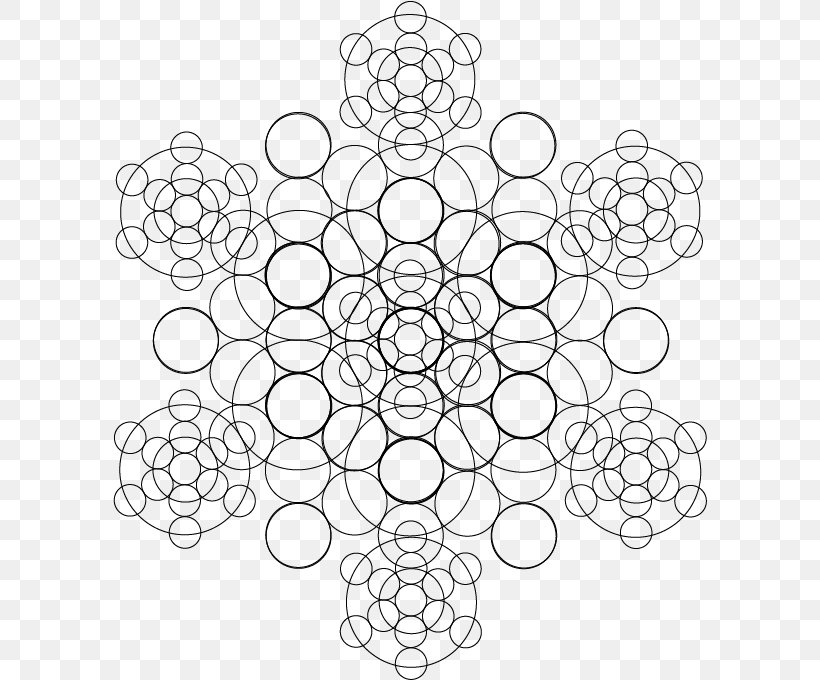
Sadece basit bir eşkenar üçgen, daire ya da kırık bir çizginin tekrarlanması bile yukarıdaki şekilleri yaratabiliyorsa, daha karmaşık şekillerin yaratabileceği varyasyon, sonsuz sayıda değişik, inanılmaz güzel ya da inanılmaz çirkin örnekler oluşturabiliyor. Fraktal geometrinin yapabilecekleri basit şekillerle sınırlı değil. Canlı cansız doğadaki her varlığın ana yapısında görmek mümkün. Biraz doğadan örnek verelim.

Mineraller

Bitkiler

Bitkiler için o kadar çok ve göz alıcı örnek var ki inanın seçmekte çok zorlandım.

Mantarlar

Hayvanlar

Doğadaki canlı cansız, bitki, hayvan, kar tanesi, buz kristali, her şey yaradılışının özü olan şeklin atom atom, hücre hücre kendi kendini milyarlarca kere tekrarlaması ile meydana geliyor. Şeklin bütünündeki desen özündeki desenin aynısı ya da çok benzeri.

Bir Şey değişir Her Şey Değişir…

Bir şekil seçiliyor daha sonrasında tekrar yapısı ile ilgili bir kural – fonksiyon – kuruluyor, dönme açısı ve tekrar sayısı belirleniyor. Bu sayede kendi kendini tekrar eden ana şekil yeni desenler çıkarıyor.

Aşağıda aynı fonksiyona ve başlangıç şekline sahip üç fraktal göreceksiniz. Başlangıç şeklinin ne kadar sıradan ve şekilsiz olduğuna dikkatinizi çekmek istiyorum. Bu üç örnek arasındaki tek fark, dönüş açısını belirleyen değerin üçünde de farklı olması. Yani aynı şekil, aynı fonksiyon ancak açı farklı… Dönüş açısının sadece bir derece değişmesi bile inanılmaz değişiklikler yaratıyor.

30 derece. Bu kadar biçimsiz ve asimetrik bir şekilden düzenli çiçek benzeri bir şeklin çıkması mucize gibi…

29 derece. Sadece bir derece değişti ama çiçek yerine sanki çiçekten bir kolye oluştu. Sadece bir derece değişikliğin sebep olduğu değişiklik inanılmaz boyutta…

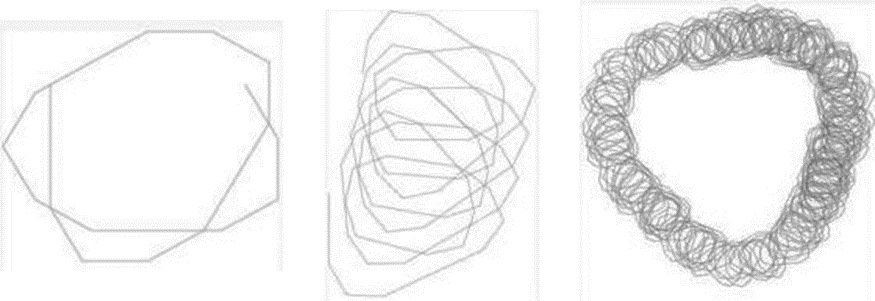
3 derece…

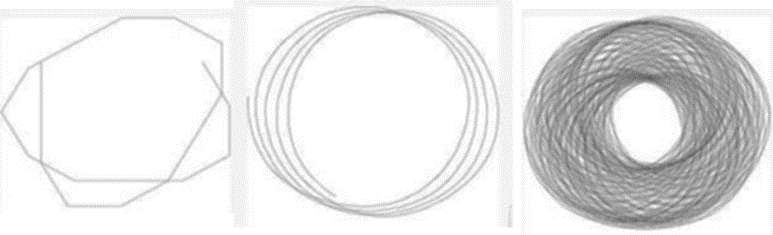
Benoit Mandelbrot, fraktal geometriyi gerçek anlamda bilgisayar ortamına ilk taşıyan matematikçi. Yukarıdaki formülü denemiş. Aslında fonksiyon bu kadar basit olsa da çok kapsamlı matematiksel alt kümeleri var, negatif ve kompleks sayıları da içeriyor ancak prensip olarak yukarıdakilerle aynı. Kendini tekrardan ibaret.

Reference:

Dikkat ettiyseniz aynı formül tekrar etmesine rağmen tekrar ettikçe şekil değişiyor, alt unsurlar denizatı, spiral gibi şekiller alıyor ancak dönüp dolaşıp yine başlangıçtaki şekle ulaşılıyor.

Fraktal geometri canlı cansız bütün varlıkların yapı taşında var. Doğadaki her şey bir fraktal fonksiyon. Başlangıçtaki şekil, tekrar sayısına göre sonsuz sayıdaki varyasyonda sonsuz farklı kendine özgü şekle bürünebiliyor.

“Gereklilik, ağırlık ve değer birbirinden ayrılmaz biçimde örülmüş üç kavramdır; sadece gereklilik ağırdır ve sadece ağır olan şey değerlidir.” 

Kundera kitabına Nietzsche’nin ‘ebedi yinelenme’ doktrini ile başlıyor. Doğada var olan her şey zaman içinde dönüşerek kendi kendini tekrar eder. Her tekrar kendisinde bir öncekinden bir şeyler barındırır. Yaşadığımız hayat daha önceki dönüşümlerin birikimlerini de içinde barındırır. Kundera birikimden kaynaklı varlığımızın ağırlığından kurtulmak adına bağlarımızdan, tabulardan ve ilişkilerden kurtulmanın varlığı hafifleteceğini öngörür.

Basit bir geometrik şekil “hafif” ya da Milan Kundera’nın tanımı ile değersiz olsa da şeklin çok sayıda tekrar edilmesi onu ağırlaştırıyor. Ağırlaşan şey değerli, işlevsel ve gerekli hale geliyor. Varlığını algıladığımız değerli, ağır ve gerekli her şeyin özünde aslında dayanılmaz bir hafiflik var.

Okumaya Devam et…